Экстремумы функции

Экстремумы функции — это такие значения аргумента, при которых функция достигает наибольшего или наименьшего значения в некоторой окрестности. Иначе говоря, это точки «взлета» и «падения» графика, где функция делает «поворот» — из роста в убывание или наоборот.

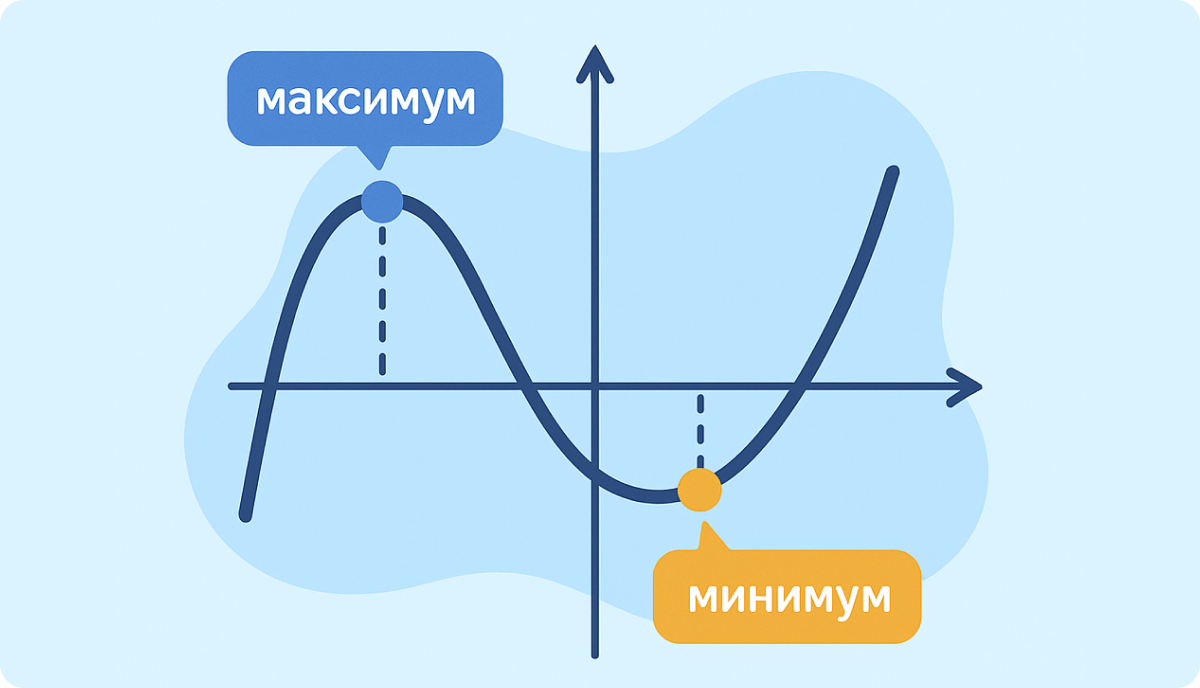
Экстремумы делятся на два типа:

• Точки максимума — в них значение функции больше, чем у всех соседних точек;
• Точки минимума — в них значение функции меньше, чем у всех ближайших значений.
  

Обе эти ситуации называют точками экстремума.

Пример:

Функция сначала растет, потом начинает убывать. Переходный момент — это локальный максимум.

Если наоборот — сначала убывает, потом начинает расти — в такой точке находится локальный минимум.

Важно:

• Экстремум может быть локальным (в пределах некоторого интервала) или глобальным (на всем множестве значений).
  
• Чтобы найти экстремум, часто используют производную: если в точке производная равна нулю и меняет знак — это потенциальный экстремум.
  
• Не каждая точка с нулевой производной — экстремум. Иногда это точка перегиба, поэтому важен анализ знаков производной до и после.
  

Зачем это нужно?

Понимание экстремумов важно:

• при решении задач оптимизации (максимум прибыли, минимум затрат),
• при анализе графиков функций,
• в физике, экономике, информатике — где нужно оценить поведение систем.

Обучайтесь программированию,
дизайну или школьным предметам
одновременно, без доплат!

Запишите ребёнка на бесплатный урок!
Определим его интересы и разработаем гибкий
план обучения.

Экстремумы в школьной программе 

В школьной программе понятие экстремумов впервые подробно изучается в 10–11 классе на уроках алгебры и математического анализа. Школьнику важно понимать, что экстремумы — это не просто «вершинки» на графике, а точки, в которых функция изменяет свое направление: с роста на убывание или наоборот. 

Чтобы находить такие точки, нужно уметь находить производную функции, решать уравнение f’(x) = 0, и анализировать, как производная ведет себя по соседству с этой точкой. 

Кроме технических навыков, важно научиться интерпретировать экстремумы: что значит максимум или минимум в конкретной задаче — будь то экономика, геометрия или физика. Это помогает не только решать типовые задачи, но и понимать, как математика работает в жизни.