Квадрат суммы и разности

Квадрат суммы и разности — это удобные формулы, которые позволяют быстро возводить в квадрат выражения вроде (a + b)² или (a – b)², не раскрывая скобки вручную.

Если проще: это математические шпаргалки, которые экономят время и показывают, как работает умножение скобок на себя.

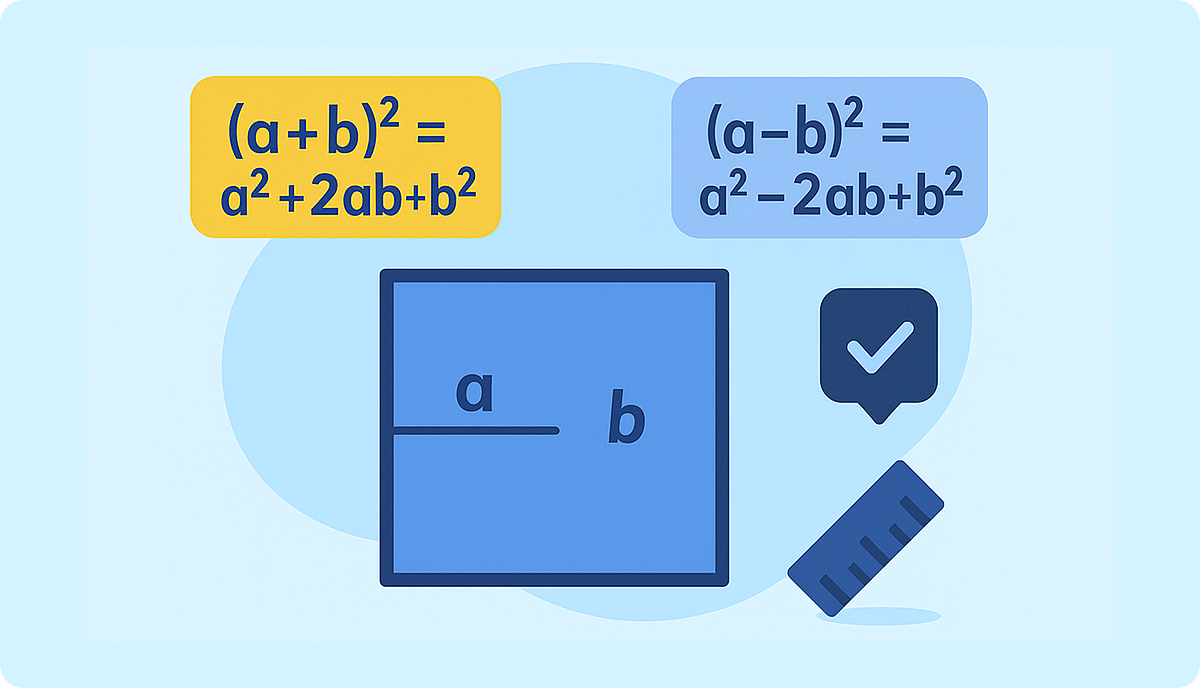
Формулы квадрата суммы и разности

Квадрат суммы:

    (a + b)² = a² + 2ab + b²

Квадрат разности:

    (a – b)² = a² – 2ab + b²

Эти формулы можно использовать в двух случаях:
— чтобы упростить выражение (например, в алгебре),
— чтобы быстро вычислить квадрат числа в уме (например, (100 – 3)² = 9409).

Примеры:

1. (x + 4)² = x² + 8x + 16
2. (3y – 2)² = 9y² – 12y + 4
3. (10 + 1)² = 100 + 20 + 1 = 121
   

Формула сработает даже с отрицательными числами или буквами — главное, правильно определить a и b, и не забыть знак в середине.

Получите до 5 уроков по математике в подарок

1. Запишите ребенка на первый пробный урок
2. Оплатите пакет занятий в течение 24 часов
3. Получите до 5 уроков в подарок

Какие бывают задачи на квадрат суммы и разности

Формулы квадрата суммы и разности — это не просто алгебраическая «фишка». Они встречаются в самых разных задачах — от простого раскрытия скобок до сложных уравнений и даже устного счёта. Вот основные типы:

1. Прямое раскрытие скобок

Это классические задания: раскрыть квадрат выражения с помощью формулы.

Примеры:

• (x + 7)² → x² + 14x + 49
• (2a – 3b)² → 4a² – 12ab + 9b²

Такие задачи хорошо тренируют механическое применение формулы и внимание к знакам.

2. Свернуть выражение в квадрат

Здесь всё наоборот: выражение уже раскрыто, и нужно узнать, что было в скобках.

Примеры:

• x² + 6x + 9 → (x + 3)²
• 9a² – 12a + 4 → (3a – 2)²

Это похоже на разгадывание уравнения назад — развивает алгебраическую интуицию.

3. Решение уравнений с квадратами

Иногда уравнение выглядит так:

(x – 5)² = 49

Здесь удобно не раскрывать скобки, а сразу извлечь корень:

x – 5 = ±7 → x = 12 или x = –2

Такие задачи учат выбирать оптимальный способ решения, а не просто «всё раскрыть».

4. Устные вычисления с формулой

Формулы можно использовать для быстрого счёта в уме!

Примеры:

• (100 + 2)² = 100² + 2×100×2 + 4 = 10404
• (10 – 1)² = 100 – 20 + 1 = 81

Это не только полезно, но и впечатляет — особенно на олимпиадах или в быту.

5. Преобразование выражений в текстовых задачах

Иногда формула помогает упростить сложное выражение, например:

• (a + b)² + (a – b)²
• (x + 1)² – (x – 1)²
  

В таких задачах нужно узнать, какие формулы подойдут, и упростить результат. Это уже алгебра «на продвинутом уровне».

__________________

В Айтигенио мы учим не просто решать задачи — а видеть суть выражений, выбирать лучший способ и действовать уверенно.

На уроках мы разбираем и классические задачи, и те, что вызывают «ступор», объясняя на простом языке, с примерами и опорой на смысл.

__________________

Обучайтесь программированию,
дизайну или школьным предметам
одновременно, без доплат!

Запишите ребёнка на бесплатный урок!
Определим его интересы и разработаем гибкий
план обучения.

Когда в школе изучают квадрат суммы и разности

Тема появляется в 7 классе, но используется ещё долго:

• при решении уравнений
• при подготовке к ОГЭ и ЕГЭ
• в олимпиадах, доказательствах, текстовых задачах

Формулы сокращённого умножения — это один из ключей к тому, чтобы полюбить алгебру как систему, а не набор правил.