Куб суммы и разности

Куб суммы и разности — это формулы, которые позволяют быстро возводить в третью степень выражения вида (a + b)³ и (a – b)³.

Если проще: куб суммы и куб разности — это удобные математические шаблоны, которые помогают упростить длинные и запутанные вычисления. Это как если бы вы заранее знали, во что превратится тройное умножение скобок.

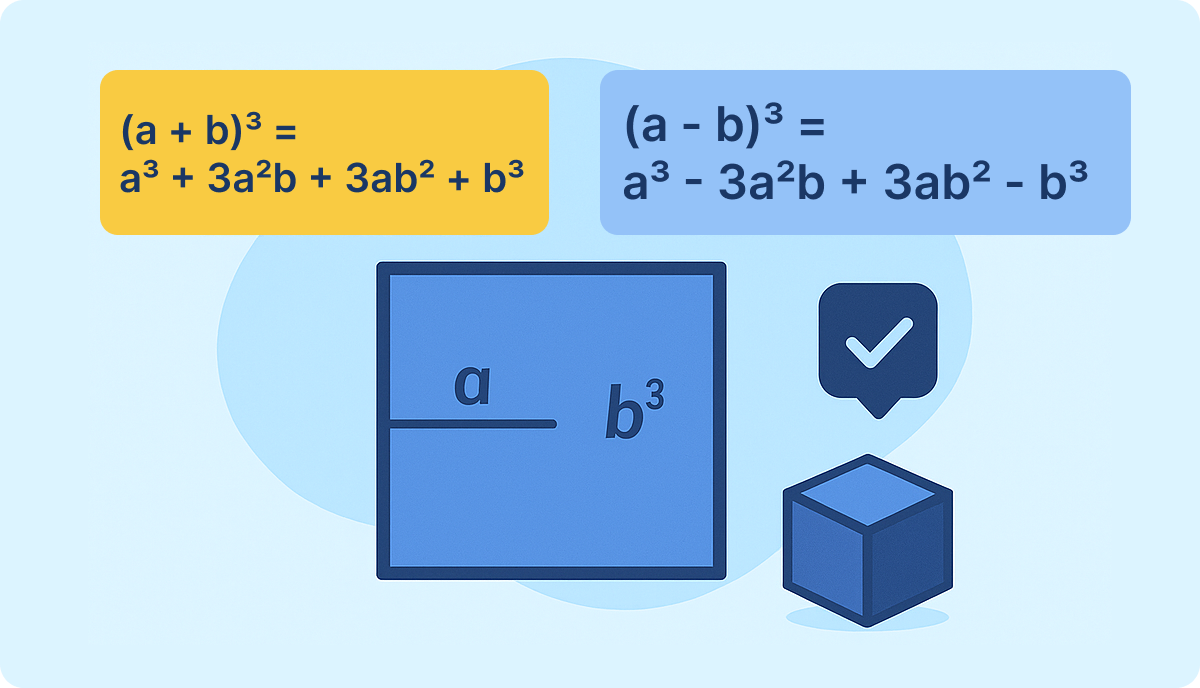
Формулы куба суммы и куба разности

Куб суммы:

    (a + b)³ = a³ + 3a²b + 3ab² + b³

Куб разности:

    (a – b)³ = a³ – 3a²b + 3ab² – b³

Эти формулы можно запомнить по «лесенке степеней» — степени у a убывают, у b растут, а коэффициенты: 1 — 3 — 3 — 1.

Пример:

(x + 2)³ = x³ + 3x²·2 + 3x·2² + 2³ = x³ + 6x² + 12x + 8

(y – 5)³ = y³ – 15y² + 75y – 125

Почему это работает?

Когда вы умножаете (a + b) на само себя три раза, это превращается в:

(a + b)(a + b)(a + b)

Вручную это занимает много времени и легко запутаться. Формула куба сокращает путь и показывает, как красиво «распадается» результат.

Так же, как квадрат суммы делит площадь на части, куб суммы раскладывает объём на объём одного, удвоенные объёмы взаимодействия и объём второго слагаемого.

Подсказка от Айтигенио: как легко запомнить формулы куба суммы и разности

Иногда формулы выглядят пугающе — особенно если в них много членов и переменных. Но есть несколько приёмов, которые помогут вам (и вашему ребёнку) понять и запомнить их без зубрёжки:

1. Обратите внимание на «лесенку степеней»:

В каждом члене формулы сумма степеней равна 3:
a³, a²b, ab², b³

Это как будто ступеньки, где один множитель уменьшается, а другой — растёт.

2. Коэффициенты всегда одинаковые:
Запомните числовую последовательность: 1 — 3 — 3 — 1

Это как «симметричная обёртка» формулы — удобно держать в голове и быстро узнавать.

3. Формулы похожи, только меняются знаки:

• В кубе суммы все знаки положительные:
    (a + b)³ = a³ + 3a²b + 3ab² + b³
  
• В кубе разности знаки чередуются:
    (a – b)³ = a³ – 3a²b + 3ab² – b³

Совет: представьте себе «волны» — положительные и отрицательные — чтобы запомнить знак каждого слагаемого.

4. Не раскрывайте скобки вручную, если не нужно

Если вы узнали, что перед вами куб суммы или разности, используйте формулу — это сократит путь к решению в разы и поможет избежать ошибок.

Получите до 5 уроков по математике в подарок

1. Запишите ребенка на первый пробный урок
2. Оплатите пакет занятий в течение 24 часов
3. Получите до 5 уроков в подарок

Где встречается куб суммы и разности?

• При упрощении выражений в алгебре.
• В уравнениях с кубами, которые легче решать с помощью форму.
• В производных и интегралах — на более старших этапах.
• В физике и экономике, когда работают с изменениями объёма или скорости в кубе.

Какие бывают задачи на куб суммы и разности

1. Прямое раскрытие скобок по формуле
    (2x + 3)³ → ?
   
2. Свернуть в формулу
    a³ + 3a²b + 3ab² + b³ → (a + b)³
   
3. Решение уравнений
    (x – 1)³ = 8 → x – 1 = 2 → x = 3
   
4. Быстрые вычисления в уме
    (10 + 1)³ = 1000 + 300 + 30 + 1 = 1331

Когда изучают куб суммы и разности

Обычно — в 7 классе, как продолжение темы формул сокращённого умножения. Эти формулы встречаются:

• при решении уравнений третьей степени
• в преобразованиях алгебраических выражений
• в заданиях на ОГЭ и ЕГЭ
• в олимпиадах и сложных примерах, где счёт вручную слишком громоздкий