Четырёхугольники. Виды четырёхугольников

Четырёхугольники — это геометрические фигуры, у которых четыре стороны, четыре угла и четыре вершины.

Если проще: это любая фигура, у которой можно обвести по контуру четыре соединённые линии, не отрывая карандаша. Самые известные примеры — прямоугольник, квадрат, ромб и трапеция.

Когда вы смотрите на экран телефона, окно, стол, плитку на кухне или страницу тетради — почти всегда вы видите четырёхугольник. Это одна из самых распространённых фигур в жизни и в геометрии.

Основные признаки четырёхугольника

• 4 стороны (отрезки, соединяющие вершины)
  
• 4 угла (в точках соединения сторон)
  
• Сумма всех углов всегда равна 360°
  
• Фигура плоская и замкнутая
  

Чтобы получился четырёхугольник, линии должны соединяться, а не расходиться.

Виды четырёхугольников

Четырёхугольники делятся на выпуклые и невыпуклые, но чаще всего в школе изучают выпуклые — те, у которых все углы меньше 180° и стороны не загибаются внутрь.

Вот основные выпуклые четырёхугольники:

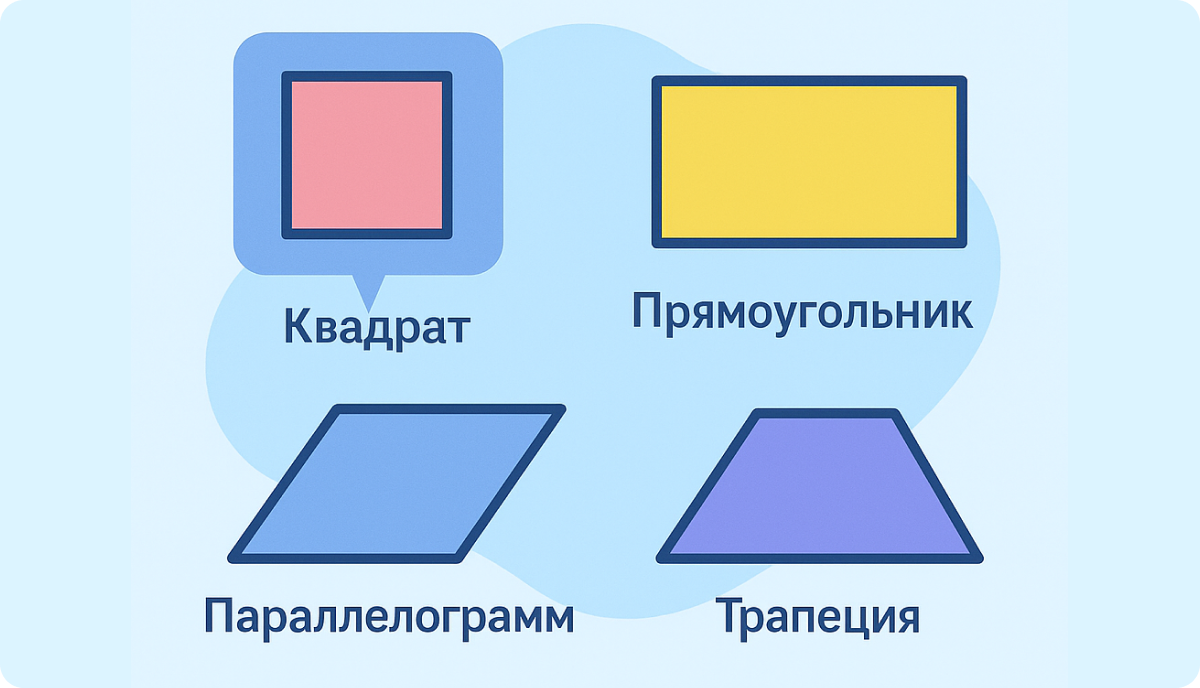
1. Параллелограмм

• Противоположные стороны параллельны и равны
• Противоположные углы — тоже равны
• Пример: наклонённая рамка картины

2. Прямоугольник

• Частный случай параллелограмма
• Все углы — прямые (по 90°)
• Противоположные стороны равны
• Пример: экран, лист бумаги, окно

3. Ромб

• Все стороны равны, но углы могут быть острыми и тупыми
• Диагонали перпендикулярны
• Пример: украшения, плитка, витражи

4. Квадрат

• Идеальный четырёхугольник: все стороны и углы равны
• Это и ромб, и прямоугольник одновременно
• Пример: шахматная клетка, плитка на полу

5. Трапеция

• Только одна пара сторон параллельна
• Уголки могут быть разными
• Бывает прямоугольная, равнобокая, обычная
• Пример: наклонная скамейка, чертёж крыши

Подсказка от Айтигенио: как отличить фигуры друг от друга

• У прямоугольника — углы ровные
• У ромба — все стороны равны, но углы не обязательно
• У трапеции — только одна пара сторон параллельна
• У параллелограмма — 2 пары параллельных сторон, но углы не 90°
• Квадрат — чемпион: всё у него равное!

Обучайтесь программированию,
дизайну или школьным предметам
одновременно, без доплат!

Запишите ребёнка на бесплатный урок!
Определим его интересы и разработаем гибкий
план обучения.

Какие есть теоремы и задачи о четырёхугольниках

Тема четырёхугольников в школе — это не только запоминание, как выглядят квадрат, ромб или трапеция. Это ещё и важные свойства, которые нужно уметь применять в задачах: на доказательство, построение, нахождение углов, сторон и площадей.

Основные теоремы о четырёхугольниках

1. Сумма углов любого четырёхугольника равна 360°
Это базовая теорема. Её используют во всех задачах, где нужно найти неизвестный угол.

2. В параллелограмме:

• Противоположные стороны равны и параллельны
• Противоположные углы равны
• Диагонали пересекаются и делятся пополам

3. В прямоугольнике:

• Диагонали равны
• Углы — по 90°

4. В ромбе:

• Все стороны равны
• Диагонали перпендикулярны
• Диагонали делят углы пополам

5. В квадрате:

• Совмещаются все свойства прямоугольника и ромба

6. В равнобедренной трапеции:

• Углы при основании равны
• Диагонали равны по длине

Примеры школьных задач

🔷 Задачи на нахождение углов:
В ромбе один угол равен 60°. Найдите остальные три.
(Ответ: 60°, 120°, 60°, 120°)

🔷 Задачи на доказательство:
Докажите, что диагонали параллелограмма делятся пополам.

🔷 Задачи на построение:
Постройте четырёхугольник, у которого два противоположных угла по 100°, а два других — по 80°.

🔷 Задачи на площади:
Найдите площадь ромба, если его диагонали равны 8 см и 6 см.
(Формула: S = (d₁ × d₂) / 2 = 24 см²)

🔷 Задачи с уравнениями:
В трапеции известно, что верхнее основание в 2 раза меньше нижнего. Найдите длину оснований, если периметр — 36 см.

В Айтигенио мы учим видеть в задаче закономерность, выбирать нужную теорему и применять её с уверенностью. Упор не на сухую теорию, а на понимание, как работают фигуры в пространстве и на чертеже.

Попробуйте бесплатное занятие — и даже сложные задачи на четырёхугольники станут понятным пазлом!

Когда в школе изучают четырёхугольники

Тема появляется в 5–6 классе и продолжается в 7 классе при изучении площадей, периметров и признаков фигур. Знание видов четырёхугольников нужно для:

• решения геометрических задач
• подготовки к ОГЭ и ЕГЭ
• построения чертежей и схем
• участия в олимпиадах и конкурсах по математике