Средняя линия треугольника

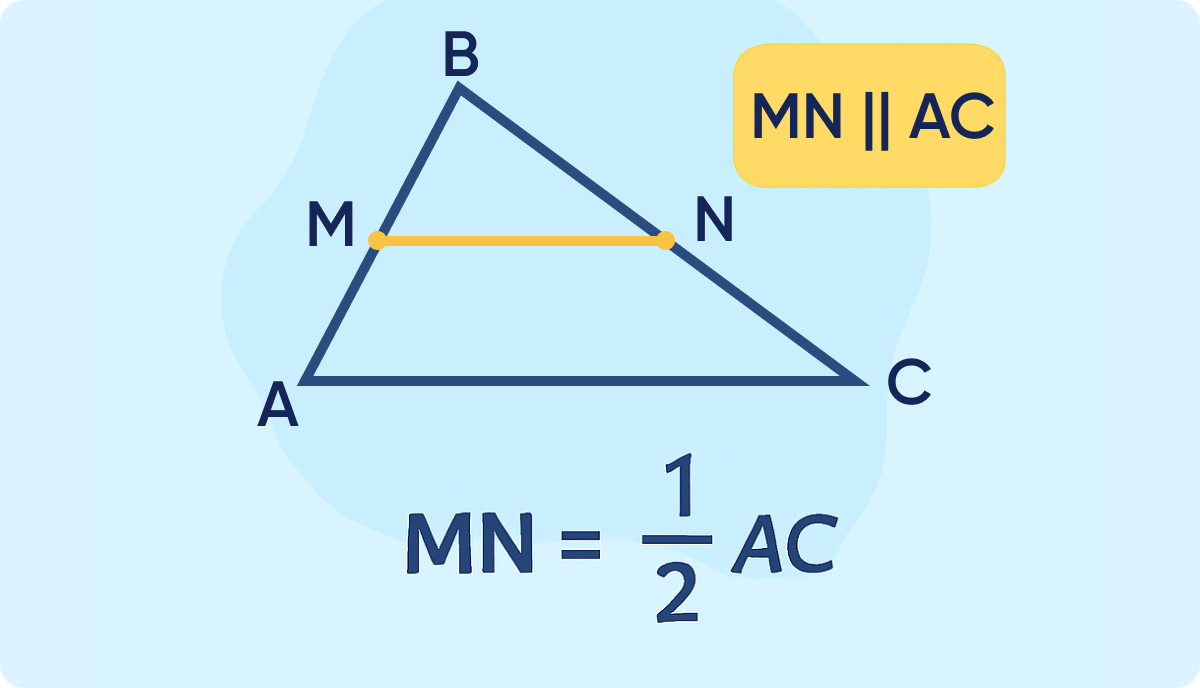
Средняя линия треугольника — это отрезок, который соединяет середины двух сторон треугольника.

Если говорить проще: вы берёте по одной точке с каждой стороны треугольника, но именно в середине, и соединяете их — получается средняя линия. Причём она не просто «соединяет» — у неё есть особые свойства, которые работают всегда.

Главные свойства средней линии

1. Параллельна третьей стороне

Средняя линия всегда лежит строго параллельно той стороне треугольника, с которой она не соединена.

2. В два раза короче этой стороны

Если основание треугольника 10 см, то средняя линия, проведённая напротив — ровно 5 см.

Эти свойства делают среднюю линию удобным инструментом в задачах: её можно использовать для построений, доказательств и вычислений.

Какие бывают задачи на среднюю линию треугольника

Задачи на среднюю линию — это отличный способ потренировать логику, пространственное мышление и внимательность. Они могут быть как базовыми, так и олимпиадного уровня.

Вот основные типы:

• Найти длину средней линии

Если известна длина стороны треугольника, к которой средняя линия параллельна, — просто делим её пополам.
Пример: сторона BC = 12 см → средняя линия = 6 см

• Найти сторону треугольника по средней линии

Работает в обратную сторону: если средняя линия 4 см, то сторона, к которой она параллельна, равна 8 см.

• Доказать, что отрезок — средняя линия

Нужно показать, что он соединяет середины двух сторон и параллелен третьей.

• Найти периметр или площадь фигуры с использованием средней линии

Такие задачи усложняются, если средняя линия входит в состав других фигур (например, в трапеции или в комбинированной фигуре).

• Построить среднюю линию

Часто встречается в задачах с циркулем и линейкой: надо найти середины сторон и аккуратно соединить их.

Изучайте математику, геометрию
и другие школьные предметы
одновременно, без доплат!

Запишите ребёнка на бесплатный урок!
Определим его интересы и разработаем гибкий
план обучения.

Какие бывают сложности с пониманием темы

Даже при простом определении средней линии у учеников могут возникать затруднения. Вот с чем чаще всего сталкиваются:

Путают середину и произвольную точку

Иногда ребёнок соединяет просто «какие-то точки на сторонах» — и получается не средняя линия, а произвольный отрезок.

Не проверяют параллельность

Важно не только соединить середины, но и понимать, почему линия параллельна третьей стороне. Без осознанного подхода это выглядит как «магия», а не математика.

Трудно применить формулу в сложной задаче

Когда средняя линия не отдельно, а встроена в большую фигуру (например, в трапецию), ученики теряются, где искать стороны и что с чем связано.

Ошибаются в построении

Если середины определены неточно — средняя линия получается «кривой», и все расчёты идут не туда.

Как мы решаем эти сложности в Айтигенио

• Показываем визуально, как выглядит настоящая средняя линия, а как — нет.
• Учим мыслить геометрически: понимать, почему формула работает.
• Практикуем в интерактивных задачах, где ребёнок сам ставит точки, тянет отрезки и сравнивает.
• Объясняем на реальных примерах: как разделить треугольник пополам, как найти короткий путь, как построить мост через треугольное поле.

Попробуйте бесплатное занятие — и ребёнок поймёт не только что такое средняя линия, но и зачем она нужна в задачах, в жизни и в логике!

Где встречается средняя линия в задачах

• В задачах на построение
• При вычислении сторон и периметров
• В доказательствах равенства фигур и параллельности
• В подготовке к ОГЭ и ЕГЭ, особенно в части «геометрия»